圆心角定理常用于数学计算,其主要功能用来计算相关圆的弧长问题。在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦心距也相等。
圆心角定理推论过程:根据旋转的性质,将∠AOB绕圆心O旋转到∠A'OB'的位置时,显然∠AOB=∠A'OB',射线OA与OA'重合,OB与OB'重合,而同圆的半径相等,OA=OA',OB=OB',从而点A与A'重合,B与B'重合。
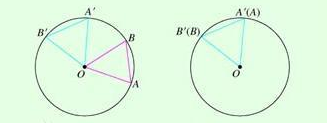
因此,弧AB与弧A'B'重合,AB与A'B'重合。即弧AB=弧A'B',AB=A'B'。则得到上面定理。
同样还可以得到:
在同圆或等圆中,如果两条弧相等,那么他们所对的圆心角相等,所对的弦相等,所对的弦心距也相等。
在同圆或等圆中,如果两条弦相等,那么他们所对的圆心角相等,所对的弧相等,所对的弦心距也相等。
所以,在同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等。
