三角形其中一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。接下来分享角平分线性质定理及证明方法。
角平分线的性质定理
1.角平分线可以得到两个相等的角。
2.角平分线上的点到角两边的距离相等。
3.三角形的三条角平分线交于一点,称作三角形内心。三角形的内心到三角形三边的距离相等。
4.三角形一个角的平分线,这个角平分线其对边所成的两条线段与这个角的两邻边对应成比例。
证明方法
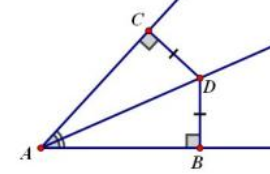
1.角平分线线上的点到角两边的距离相等。
若射线AD是∠CAB的角平分线,求证:CD=BD
∵∠DCA=∠DBA
∠CAD=∠BAD
AD=AD
∴△ACD≌△ABD
∴CD=BD
2.三角形内角平分线分对边所成的两条线段,和两条邻边成比例
在三角形ABC中,当AD是顶角A的角平分线交底边于D时,BD/CD=AB/AC。
证明:
如图,AD为△ABC的角平分线,过点D向边AB,AC分别引垂线DE,DF.则DE=DF。
S△ABD:S△ACD=BD/CD
又因为S△ABD:S△ACD=[(1/2)AB×DE]:[(1/2)AC×DF]=AB:AC
所以BD/CD=AB/AC。
