初中所学的函数包括一次函数、反比例函数、二次函数,函数在考试中占有很高的分值。因此,小编整理了它们的一些重要知识点。
一次函数
一、定义:一般地,解析式形如y=kx+b(k、b是常数,且k≠0)的函数叫做一次函数。一次函数的定义域是一切实数。当b=0时,y=kx(k≠0)是正比例函数。
二、图像
1、正比例函数y=kx(k≠0,k是常数)的图像是经过O(0,0)和M(1,k)两点的一条直线。
(1)当k>0时,图像经过原点和第一、三像限;

(2)当k<0时,图像经过原点和第二、四像限:

2、一次函数y=kx+b(k是常数,k≠0)的图像是经过A(0,b)和B(-k/b,0)两点的一条直线,当k、b≠0时,图像(即直线)的位置分4种不同情况:
(1)k>0,b>0时,直线经过第一、二、三像限:
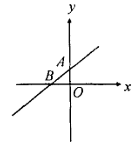
(2)k>0,b<0时,直线经过第一、三、四像限:
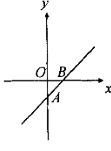
(3)k<0,b>0时,直线经过第一、二、四像限:
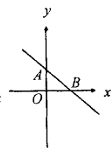
(4)k<0,b<0时,直线经过第二、三、四像限:
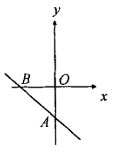
3、求一次函数的解析式
若已知一次函数的图像(即直线)经过两个已在点A(x1,y1)和B(x2,y2)求这个一次函数的解析式,其方法和步骤是:
(1)设一次函数的解析式:y=kx+b(k≠0)
(2)将A、B两点的坐标代入所设函数的解析式,得两个方程:y1=kx1+b ① ;y2=kx2+b ②
(3)联立①②解方程组,从而求出k、b值。
这一先设系数k、b,从而通过解方程求系数的方法,称为待定系数法。
反比例函数
一、定义:一般地,形如y=k/x(k是常数,k≠0)的函数叫做反比例函数。
(1)常数k称为比例系数,k ≠0、x≠0、y≠0;
(2)判断一个函数是否是反比例函数,关键是看两个变量的乘积是否是一个常数;
(3)解析式有三种常见的表达形式:
(A)y = k/x(k≠0);(B)xy = k(k≠0);(C)y=kx-1(k≠0)
二、图像
1、k>0时
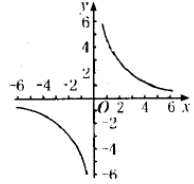
2、k<0时
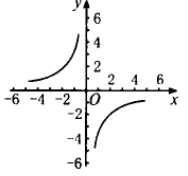
二次函数
一、定义:一般地,形如y=ax2+bx+c的函数,叫做二次函数。
这里需要强调:a、b、c为常数并且a≠ 0;最高次数为2;代数式一定是整式。
二、基本形式及图像
1、y=ax2
(1)a>0时:开口方向向上,顶点坐标(0,0),对称轴为y轴。x>0时,y随x的增大而增大;x<0时,y随x的增大而减小;x=0时,y有最小值0。
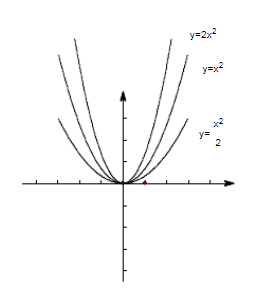
(2)a<0时,开口方向向下,顶点坐标(0,0),对称轴为y轴。x>0时,y随x的增大而减小;x<0时,y随x的增大而增大;x=0时,y有最大值0。
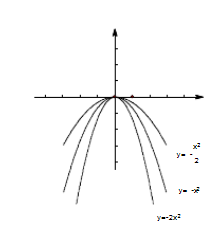
2、y=ax2+c
(1)a>0时:开口方向向上,顶点坐标(0,c),对称轴为y轴。x>0时,y随x的增大而增大;x<0时,y随x的增大而减小;x=0时,y有最小值0。
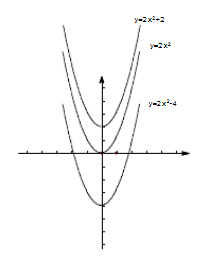
(2)a<0时,开口方向向下,顶点坐标(0,c),对称轴为y轴。x>0时,y随x的增大而减小;x<0时,y随x的增大而增大;x=0时,y有最大值0。
3、y=a(x-h)2
(1)a>0时:开口方向向上,顶点坐标(h,0),对称轴为x=h。x>h时,y随x的增大而增大;x<h时,y随x的增大而减小;x=h时,y有最小值0。
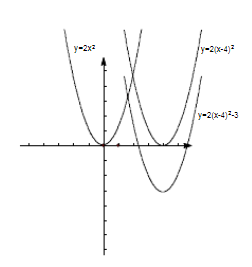
(2)a<0时:开口方向向下,顶点坐标(h,0),对称轴为x=h。x>h时,y随x的增大而减小;x<h时,y随x的增大而增大;x=h时,y有最大值0。
4、y=a(x-h)2+k
(1)a>0时:开口方向向上,顶点坐标(h,k),对称轴为x=h。x>h时,y随x的增大而增大;x<h时,y随x的增大而减小;x=h时,y有最小值k。
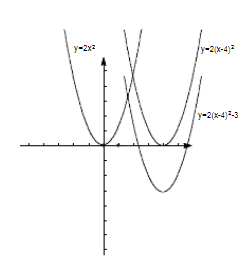
(2)a<0时:开口方向向下,顶点坐标(h,k),对称轴为x=h。x>h时,y随x的增大而减小;x<h时,y随x的增大而增大;x=h时,y有最大值k。
以上是小编整理的函数的知识点,希望能帮到你。
