圆内接四边形是一个几何概念,四边形的四个顶点均在同一个圆上的四边形叫做圆内接四边形,下面我们就来看看它有什么样的性质。
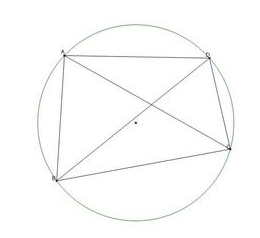
以圆内接四边形ABCD为例,圆心为O,假设AC、BD交于Q,则:
1、圆内接四边形的对角互补:∠BAD+∠DCB=180°,∠ABC+∠ADC=180°
2、圆内接四边形的任意一个外角等于它的内对角:∠CBE=∠ADC
3、圆心角的度数等于所对弧的圆周角的度数的两倍:∠AOB=2∠ACB=2∠ADB
4、圆内接四边形对应三角形相似:△ABQ∽△DCQ
5、同弧所对的圆周角相等:∠ABD=∠ACD
6、相交弦定理:AQ×CQ=BQ×DQ
7、托勒密定理:AB×CD+AD×CB=AC×BD
8、判定定理编辑
1、如果一个四边形的对角互补,那么这个四边形内接于一个圆。
2、如果一个四边形的外角等于它的内对角,那么这个四边形内接于一个圆。
3、如果一个四边形的四个顶点与某定点等距离,那么这个四边形内接于以该点为圆心的一个圆。
4、若有两个同底的三角形,另一顶点都在底的同旁,且顶角相等,那么这两个三角形有公共的外接圆。
5、如果一个四边形的张角相等,那么这个四边形内接于一个圆。
